Table of contents

0. Functions7h 52m
1. Limits and Continuity2h 2m
2. Intro to Derivatives1h 33m
3. Techniques of Differentiation3h 18m
4. Applications of Derivatives2h 38m
5. Graphical Applications of Derivatives6h 2m
6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
7. Antiderivatives & Indefinite Integrals1h 26m
8. Definite Integrals4h 44m
9. Graphical Applications of Integrals2h 27m
- Area Between Curves
  1h 18m
- Introduction to Volume & Disk Method
  1h 8m
10. Physics Applications of Integrals 3h 16m
- Kinematics
  1h 13m
- Work
  2h 3m
11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 34m
12. Techniques of Integration7h 39m
13. Intro to Differential Equations2h 55m
14. Sequences & Series5h 36m
15. Power Series2h 19m
- Introduction to Power Series
  1h 9m
- Taylor Series & Taylor Polynomials
  1h 10m
16. Parametric Equations & Polar Coordinates7h 58m

1. Limits and Continuity

Continuity

Calculus

1. Limits and Continuity

Continuity

Previous problemNext problem

2:25 minutes

Problem 53a

Textbook Question

Where is the function continuous? Differentiable? Use the graph of f in the figure to do the following. <IMAGE>
a. Find the values of x in (0, 3) at which f is not continuous.

Verified step by step guidance

Identify the definition of continuity: A function f(x) is continuous at a point x = c if the following three conditions are met: 1) f(c) is defined, 2) the limit of f(x) as x approaches c exists, and 3) the limit of f(x) as x approaches c is equal to f(c).

Examine the graph of the function f in the interval (0, 3) to identify any points where the function might not be continuous. Look for any breaks, jumps, or holes in the graph.

For each point of interest identified in the previous step, check if f(x) is defined at that point. If f(x) is not defined, the function is not continuous at that point.

Next, check if the limit of f(x) as x approaches the point from both the left and the right exists and is equal. If the left-hand limit and the right-hand limit are not equal, the function is not continuous at that point.

Finally, verify if the limit of f(x) as x approaches the point is equal to f(c). If any of these conditions are not met, the function is not continuous at that point. List all such points in the interval (0, 3).

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above

Video duration:

Play a video:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Continuity of a Function

A function is continuous at a point if the limit of the function as it approaches that point equals the function's value at that point. This means there are no breaks, jumps, or holes in the graph of the function at that point. For a function to be continuous over an interval, it must be continuous at every point within that interval.

Differentiability of a Function

A function is differentiable at a point if it has a defined derivative at that point, which implies that the function is smooth and has no sharp corners or vertical tangents. Importantly, a function must be continuous at a point to be differentiable there, but continuity alone does not guarantee differentiability.

Identifying Discontinuities

Discontinuities in a function can occur in several forms, including removable, jump, and infinite discontinuities. To find where a function is not continuous, one must analyze the graph for any points where the function does not meet the criteria for continuity, such as breaks in the graph or undefined values. This analysis is crucial for determining the intervals of continuity and differentiability.

Watch next

Master Intro to Continuity with a bite sized video explanation from Patrick

Start learning

Related Videos

Related Practice

Textbook Question

Suppose the rental cost for a snowboard is $25 for the first day (or any part of the first day) plus $15 for each additional day (or any part of a day).

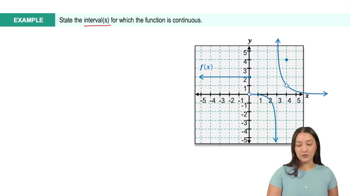
e. For what values of t is f continuous? Explain.

Textbook Question

Let $g\left(x\right)=\begin{cases}5x-2 & \text{if }x<1\\ a & \text{if }x=1\\ ax^2+bx & \text{if }x>1\end{cases}$ .

Determine values of the constants $a$ and $b$ , if possible, for which $g$ is continuous at $x equals 1$ .

Textbook Question

Complete the following sentences in terms of a limit.

a. A function is continuous from the left at a if _____.

Textbook Question

Complete the following sentences in terms of a limit.

b. A function is continuous from the right at a if _____ .

Textbook Question

Use the graph of f in the figure to do the following. <IMAGE>

a. Find the values of x in (-2,2) at which f is not continuous.

Textbook Question

Continuity of a piecewise function Let g(x) = <matrix 2x1> For what values of a is g continuous?

Textbook Question

Continuous Extension

Explain why the function ƒ(𝓍) = sin(1/𝓍) has no continuous extension to 𝓍 = 0.

Textbook Question

[Technology Exercise] In Exercises 33–36, graph the function to see whether it appears to have a continuous extension to the given point a. If it does, use Trace and Zoom to find a good candidate for the extended function’s value at a. If the function does not appear to have a continuous extension, can it be extended to be continuous from the right or left? If so, what do you think the extended function’s value should be?

g(θ) = 5 cos θ / (4θ ― 2π) , a = π/2

Show more practices

Download the Mobile app

Privacy

Do not sell my personal information

Accessibility

Patent notice

Sitemap

Where is the function continuous? Differentiable? Use the graph of f in the figure to do the following. <IMAGE>a. Find the values of x in (0, 3) at which f is not continuous.

Key Concepts

Continuity of a Function

Differentiability of a Function

Identifying Discontinuities

Watch next

Where is the function continuous? Differentiable? Use the graph of f in the figure to do the following. <IMAGE>
a. Find the values of x in (0, 3) at which f is not continuous.