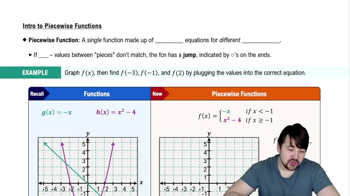
Exercises 5–10 refer to the function
f(x) = { x² − 1, −1 ≤ x < 0
2x, 0 < x < 1
1, x = 1
−2x + 4, 1 < x < 2
0, 2 < x < 3
graphed in the accompanying figure.
<IMAGE>
b. Does lim x → −1⁺ f (x) exist?
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: