Textbook Question
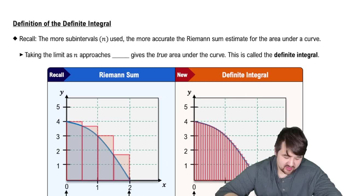
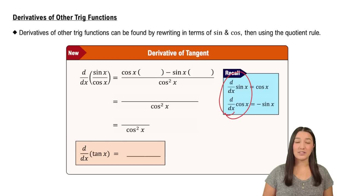
Find the function The following limits represent the slope of a curve y = f(x) at the point (a,f(a)). Determine a possible function f and number a; then calculate the limit.
(lim x🠂1) 3x²+4x-7 / x-1
2. Intro to Derivatives
Derivatives as Functions
7:29 minutesProblem 3.1.62a
Textbook Question
{Use of Tech} Approximating derivatives Assuming the limit exists, the definition of the derivative f′(a) = lim h→0 f(a + h) − f(a) / h implies that if ℎ is small, then an approximation to f′(a) is given by
f' (a) ≈ f(a+h) - f(a) / h. If ℎ > 0 , then this approximation is called a forward difference quotient; if ℎ < 0 , it is a backward difference quotient. As shown in the following exercises, these formulas are used to approximate f′ at a point when f is a complicated function or when f is represented by a set of data points. <IMAGE>
Let f (x) = √x.
a. Find the exact value of f' (4).
Verified step by step guidance1
Step 1: Recall the definition of the derivative for a function f(x). The derivative f'(x) is defined as the limit: f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}.
Step 2: Identify the function given in the problem. Here, f(x) = \sqrt{x}. We need to find the derivative at x = 4, so we are looking for f'(4).
Step 3: Substitute f(x) = \sqrt{x} into the derivative definition. This gives us: f'(4) = \lim_{h \to 0} \frac{\sqrt{4+h} - \sqrt{4}}{h}.
Step 4: Simplify the expression under the limit. To do this, multiply the numerator and the denominator by the conjugate of the numerator: \frac{\sqrt{4+h} - 2}{h} \cdot \frac{\sqrt{4+h} + 2}{\sqrt{4+h} + 2}.
Step 5: Simplify the resulting expression and evaluate the limit as h approaches 0. This will give you the exact value of f'(4).
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
7mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Definition of the Derivative
The derivative of a function at a point quantifies the rate at which the function's value changes as its input changes. Mathematically, it is defined as f′(a) = lim h→0 [f(a + h) - f(a)] / h. This limit represents the slope of the tangent line to the function at the point a, providing insight into the function's behavior near that point.
Recommended video:
05:43
Definition of the Definite Integral
Forward and Backward Difference Quotients
The forward difference quotient is an approximation of the derivative using values of the function at a point and a small increment h, expressed as f' (a) ≈ [f(a + h) - f(a)] / h for h > 0. Conversely, the backward difference quotient uses a decrement, given by f' (a) ≈ [f(a) - f(a - h)] / h for h < 0. These approximations are particularly useful for estimating derivatives when dealing with complex functions or discrete data.
Recommended video:
06:43The Quotient Rule
Calculating Derivatives of Functions
To find the exact value of the derivative for a specific function, such as f(x) = √x, one can either apply the definition of the derivative directly or use known derivative rules. For f(x) = √x, the derivative can be calculated using the power rule, where f'(x) = (1/2)x^(-1/2), allowing for straightforward evaluation at any point, such as x = 4.
Recommended video:
06:30Derivatives of Other Trig Functions
Related Videos
Related Practice