Differential Estimates of Change
In Exercises 35–40, write a differential formula that estimates the given change in volume or surface area.
The change in the surface area S = 6x² of a cube when the edge lengths change from x₀ to x₀ + dx
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: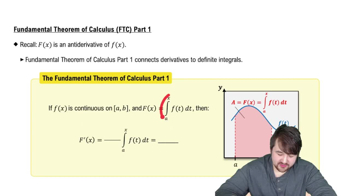


 5:53m
5:53mMaster Finding Differentials with a bite sized video explanation from Patrick
Start learning