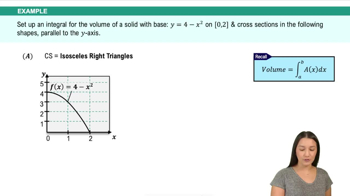
Particle motion The positions of two particles on the s-axis are s₁ = cos t and s₂ = cos (t + π/4) .
a. What is the farthest apart the particles ever get?
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: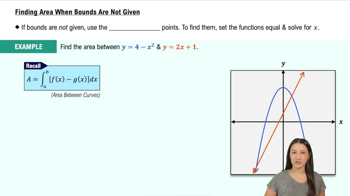


 1:13m
1:13mMaster Intro to Applied Optimization: Maximizing Area with a bite sized video explanation from Patrick
Start learning