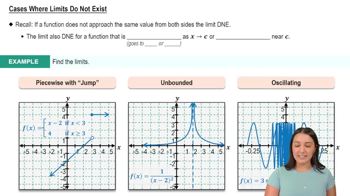
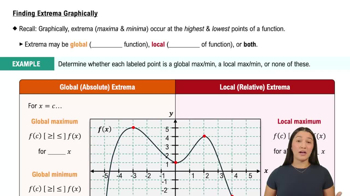
Population models The population of a species is given by the function P(t) = Kt²/(t² + b) , where t ≥ 0 is measured in years and K and b are positive real numbers.
c. For arbitrary positive values of K and b, when does the maximum growth rate occur (in terms of K and b)?