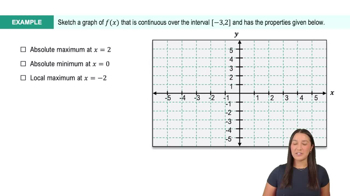
Sketch the graph of a continuous function ƒ on [0, 4] satisfying the given properties.
ƒ' (x) and ƒ'3 are undefined; ƒ'(2) = 0; has a local maximum at x= 1; ƒ has local minimum at x = 2; and ƒ has an absolute maximum at x= 3; and ƒ has an absolute minimum at x = 4 .