Evaluate the expression.
Table of contents
- 0. Functions7h 54m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 31m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
0. Functions
Inverse Trigonometric Functions
Problem 80
Textbook Question
Evaluating inverse trigonometric functions Without using a calculator, evaluate the following expressions.
tan−1(tan(43π))
 Verified step by step guidance
Verified step by step guidance1
Understand the problem: We need to evaluate \( \tan^{-1}(\tan(\frac{3\pi}{4})) \). This involves understanding the behavior of the tangent function and its inverse.
Recall the range of \( \tan^{-1}(x) \), which is \( (-\frac{\pi}{2}, \frac{\pi}{2}) \). The inverse tangent function will return an angle within this range.
Evaluate \( \tan(\frac{3\pi}{4}) \). The angle \( \frac{3\pi}{4} \) is in the second quadrant, where the tangent function is negative. Specifically, \( \tan(\frac{3\pi}{4}) = -1 \).
Now, find \( \tan^{-1}(-1) \). Since \( \tan^{-1}(x) \) returns an angle in \( (-\frac{\pi}{2}, \frac{\pi}{2}) \), we need to find an angle in this range whose tangent is \(-1\).
The angle that satisfies \( \tan(\theta) = -1 \) within the range \( (-\frac{\pi}{2}, \frac{\pi}{2}) \) is \( -\frac{\pi}{4} \). Therefore, \( \tan^{-1}(\tan(\frac{3\pi}{4})) = -\frac{\pi}{4} \).
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Inverse Trigonometric Functions
Inverse trigonometric functions, such as an^{-1} (arctan), are used to find the angle whose tangent is a given number. These functions are defined over specific ranges to ensure they are one-to-one, allowing for unique outputs. Understanding their properties and ranges is crucial for evaluating expressions involving these functions.
Recommended video:

Derivatives of Other Inverse Trigonometric Functions
Periodic Functions
Trigonometric functions like sine, cosine, and tangent are periodic, meaning they repeat their values in regular intervals. For example, the tangent function has a period of an(x + π) = tan(x). This periodicity is essential when evaluating expressions involving angles that exceed the standard range of the inverse functions.
Recommended video:
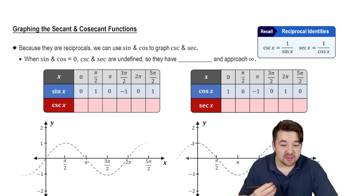
Graphs of Secant and Cosecant Functions
Angle Reduction
Angle reduction involves simplifying angles to fall within a specific range, typically between 0 and 2π for trigonometric functions. For instance,
rac{3 ext{π}}{4} can be analyzed in terms of its reference angle in the second quadrant. This technique is vital for accurately evaluating trigonometric expressions and their inverses.
Recommended video:
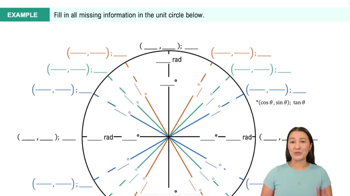
Trig Values in Quadrants II, III, & IV Example 2
Related Videos
Related Practice
Multiple Choice


