Evaluating trigonometric functions Without using a calculator, evaluate the following expressions or state that the quantity is undefined.
cos (2π/3)
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:

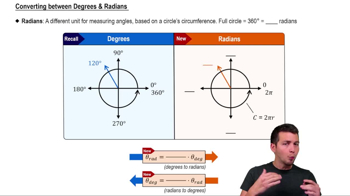

 5:4m
5:4mMaster Converting between Degrees & Radians with a bite sized video explanation from Patrick
Start learning