Absolute Extrema on Finite Closed Intervals


In Exercises 37–40, find the function’s absolute maximum and minimum values and say where they occur.


f(x) = x⁴ᐟ³, −1 ≤ x ≤ 8

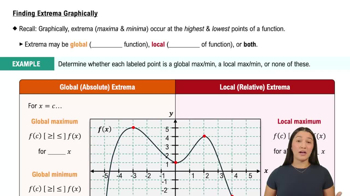
{Use of Tech} Absolute maxima and minima

a. Find the critical points of f on the given interval.

b. Determine the absolute extreme values of f on the given interval.

c. Use a graphing utility to confirm your conclusions.

f(x) = 2ᶻ sin x on [-2,6]

{Use of Tech} Critical points and extreme values

a. Find the critical points of the following functions on the given interval. Use a root finder, if necessary.

b. Use a graphing utility to determine whether the critical points correspond to local maxima, local minima, or neither.

c. Find the absolute maximum and minimum values on the given interval, if they exist

h(x) (5-x)/(x² + 2x - 3) on [-10,10]

Theory and Examples

Determine the values of constants a and b so that f(x) = ax² + bx has an absolute maximum at the point (1,2).

Absolute Extrema on Finite Closed Intervals

In Exercises 37–40, find the function’s absolute maximum and minimum values and say where they occur.

g(θ) = θ³ᐟ⁵, −32 ≤ θ ≤ 1

Absolute Extrema on Finite Closed Intervals

In Exercises 21–36, find the absolute maximum and minimum values of each function on the given interval. Then graph the function. Identify the points on the graph where the absolute extrema occur, and include their coordinates.

f(x) = (2/3)x − 5, −2 ≤ x ≤ 3

Absolute Extrema on Finite Closed Intervals

In Exercises 21–36, find the absolute maximum and minimum values of each function on the given interval. Then graph the function. Identify the points on the graph where the absolute extrema occur, and include their coordinates.

h(x) = ³√x, −1 ≤ x ≤ 8

Absolute Extrema on Finite Closed Intervals

In Exercises 21–36, find the absolute maximum and minimum values of each function on the given interval. Then graph the function. Identify the points on the graph where the absolute extrema occur, and include their coordinates.

g(x) = √(4 − x²), −2 ≤ x ≤ 1

Absolute Extrema on Finite Closed Intervals

In Exercises 21–36, find the absolute maximum and minimum values of each function on the given interval. Then graph the function. Identify the points on the graph where the absolute extrema occur, and include their coordinates.

f(t) = 2 − |t|, −1 ≤ t ≤ 3