Textbook Question
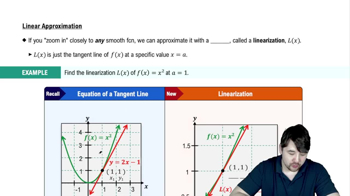
Estimating speed Use the linear approximation given in Example 1 to answer the following questions.
If you travel one mile in 59 seconds, what is your approximate average speed? What is your exact speed?
4. Applications of Derivatives
Linearization
2:30 minutesProblem 3.9.4
Textbook Question
Finding Linearizations
In Exercises 1–5, find the linearization L(x) of f(x) at x = a.
f(x) = ∛x, a = −8
Verified step by step guidance1
Identify the function f(x) = ∛x and the point of interest x = a = -8.
Recall the formula for the linearization of a function at a point: L(x) = f(a) + f'(a)(x - a).
Calculate f(a) by substituting a = -8 into the function: f(-8) = ∛(-8).
Find the derivative f'(x) of the function f(x) = ∛x. Use the power rule for derivatives: f(x) = x^(1/3) implies f'(x) = (1/3)x^(-2/3).
Evaluate the derivative at the point a = -8: f'(-8) = (1/3)(-8)^(-2/3). Substitute f(a) and f'(a) into the linearization formula to find L(x).
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Linearization
Linearization is the process of approximating a function near a given point using the tangent line at that point. The linearization of a function f(x) at x = a is given by L(x) = f(a) + f'(a)(x - a). This provides a simple linear model that approximates the function's behavior close to x = a.
Recommended video:
07:17
Linearization
Derivative
The derivative of a function, denoted as f'(x), represents the rate at which the function's value changes with respect to changes in x. It is the slope of the tangent line to the function at any given point. For linearization, the derivative at x = a, f'(a), is crucial as it determines the slope of the linear approximation.
Recommended video:
05:44Derivatives
Cube Root Function
The cube root function, f(x) = ∛x, is a type of root function where the output is the number that, when cubed, gives x. Understanding its behavior, especially around specific points like x = -8, is essential for calculating derivatives and linearizations. The function is continuous and differentiable for all real numbers, which facilitates finding its linear approximation.
Recommended video:
5:57Graphs of Common Functions
Related Videos
Related Practice