State the inputs and outputs of the following relation. Is it a function? {}
Table of contents
- 0. Functions7h 55m
- Introduction to Functions18m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 31m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
0. Functions
Introduction to Functions
Problem 112a
Textbook Question
Daylight function for 40 °N Verify that the function D(t)=2.8sin(3652π(t−81))+12 has the following properties, where t is measured in days and D is the number of hours between sunrise and sunset. It has a period of 365 days.
 Verified step by step guidance
Verified step by step guidance1
Identify the general form of a sinusoidal function, which is typically given by A \sin(B(t - C)) + D, where A is the amplitude, B affects the period, C is the phase shift, and D is the vertical shift.
In the given function D(t) = 2.8 \sin\left(\frac{2\pi}{365}(t-81)\right) + 12, compare it to the general form to identify the values of A, B, C, and D. Here, A = 2.8, B = \frac{2\pi}{365}, C = 81, and D = 12.
The period of a sinusoidal function is determined by the coefficient B in front of t. The formula for the period is \frac{2\pi}{B}.
Substitute B = \frac{2\pi}{365} into the period formula: \text{Period} = \frac{2\pi}{\frac{2\pi}{365}}.
Simplify the expression for the period to verify that it equals 365 days, confirming that the function has the desired period.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
0 Comments
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Trigonometric Functions
Trigonometric functions, such as sine and cosine, are fundamental in calculus and describe relationships between angles and sides of triangles. In the context of periodic phenomena, like daylight hours, the sine function models the cyclical nature of these changes over time, allowing us to predict values based on the angle of the input.
Recommended video:

Introduction to Trigonometric Functions
Periodicity
Periodicity refers to the repeating nature of a function over a specific interval. In this case, the function D(t) has a period of 365 days, meaning it repeats its values every year. Understanding periodicity is crucial for analyzing functions that model seasonal or cyclical behaviors, such as daylight duration throughout the year.
Recommended video:

Introduction to Tangent Graph
Phase Shift
Phase shift is a horizontal shift in the graph of a periodic function, affecting where the cycle begins. In the function D(t), the term (t - 81) indicates a phase shift, which adjusts the starting point of the sine wave. This is important for accurately modeling real-world phenomena, such as when daylight hours begin to increase or decrease throughout the year.
Recommended video:
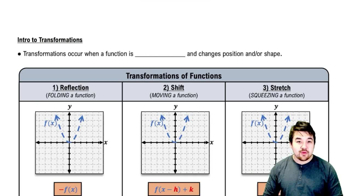
Intro to Transformations

 1:36m
1:36mWatch next
Master Introduction to Calculus Channel with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Multiple Choice
