Solving equations Solve the following equations.
ln x= -1
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: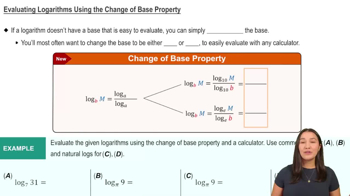

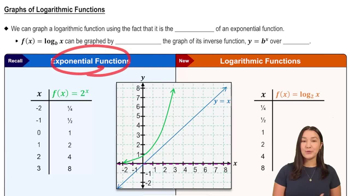

 4:46m
4:46mMaster Solving Exponential Equations Using Like Bases with a bite sized video explanation from Patrick
Start learning