The diameter of a sphere is measured as 100 ± 1 cm and the volume is calculated from this measurement. Estimate the percentage error in the volume calculation.
Table of contents
- 0. Functions7h 54m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 31m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
4. Applications of Derivatives
Differentials
Problem 51
Textbook Question
Applications
Classical accounts tell us that a 170-oar trireme (ancient Greek or Roman warship) once covered 184 sea miles in 24 hours. Explain why at some point during this feat the trireme’s speed exceeded 7.5 knots (sea or nautical miles per hour).
 Verified step by step guidance
Verified step by step guidance1
Recognize that this problem is an application of the Mean Value Theorem (MVT) from calculus, which states that for a continuous and differentiable function over a closed interval, there exists at least one point where the instantaneous rate of change (derivative) equals the average rate of change over that interval.
Define the function s(t) to represent the distance covered by the trireme at time t, where t is measured in hours and s(t) is in sea miles. The interval of interest is from t = 0 to t = 24 hours.
Calculate the average speed of the trireme over the 24-hour period. The average speed is given by the total distance traveled divided by the total time, which is 184 sea miles / 24 hours.
Apply the Mean Value Theorem: Since s(t) is continuous and differentiable over the interval [0, 24], there exists at least one time c in (0, 24) such that the derivative s'(c), representing the instantaneous speed, equals the average speed.
Compare the average speed to 7.5 knots. If the average speed is less than 7.5 knots, then at some point, the instantaneous speed s'(c) must have exceeded 7.5 knots to compensate for slower speeds at other times, ensuring the average speed is achieved.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Mean Value Theorem
The Mean Value Theorem (MVT) in calculus states that for a continuous function on a closed interval [a, b] that is differentiable on the open interval (a, b), there exists at least one point c in (a, b) where the instantaneous rate of change (derivative) equals the average rate of change over [a, b]. This theorem is crucial for proving that the trireme's speed exceeded 7.5 knots at some point during its journey.
Recommended video:
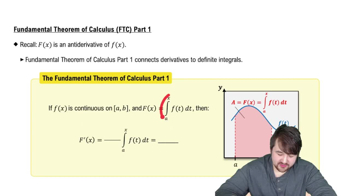
Fundamental Theorem of Calculus Part 1
Average Speed
Average speed is calculated by dividing the total distance traveled by the total time taken. In this scenario, the trireme covered 184 sea miles in 24 hours, resulting in an average speed of 184/24 = 7.67 knots. Understanding average speed helps establish a baseline to apply the Mean Value Theorem, indicating that the speed must have exceeded 7.5 knots at some point.
Recommended video:

Average Value of a Function
Instantaneous Speed
Instantaneous speed refers to the speed of an object at a specific moment in time, which can be determined by the derivative of the position function with respect to time. In the context of the trireme, the Mean Value Theorem implies that if the average speed is 7.67 knots, there must be an instant where the instantaneous speed is exactly 7.67 knots, thus exceeding 7.5 knots at some point.
Recommended video:
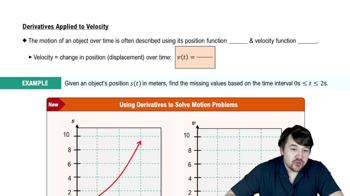
Derivatives Applied To Velocity

 5:53m
5:53mWatch next
Master Finding Differentials with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
