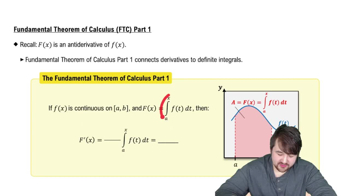
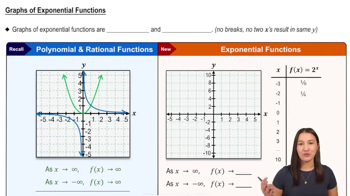
21–32. Mean Value Theorem Consider the following functions on the given interval [a, b].
a. Determine whether the Mean Value Theorem applies to the following functions on the given interval [a, b].
b. If so, find the point(s) that are guaranteed to exist by the Mean Value Theorem.
ƒ(x) = x + 1/x; [1,3]