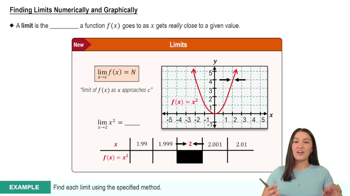
If a function f represents a system that varies in time, the existence of lim means that the system reaches a steady state (or equilibrium). For the following systems, determine whether a steady state exists and give the steady-state value.
The population of a bacteria culture is given by .