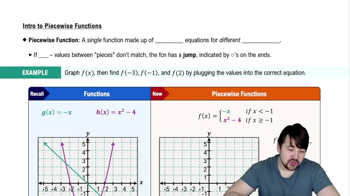
Use the graph of g in the figure to do the following. <IMAGE>
b. Find the values of x in (-2,2) at which g is not differentiable.
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:


 5:02m
5:02mMaster Determining Differentiability Graphically with a bite sized video explanation from Patrick
Start learning