Here are the essential concepts you must grasp in order to answer the question correctly.
Quotient Rule
The quotient rule is used to find the derivative of a function that is the quotient of two differentiable functions. If you have a function h(x) = f(x)/g(x), the derivative h'(x) is given by [g(x)f'(x) - f(x)g'(x)] / [g(x)]^2. This rule is essential for differentiating the given function f(x) / (g(x) + 1).
Recommended video:
Derivative Evaluation
Derivative evaluation involves substituting specific values into the derivative formula to find the rate of change at a particular point. In this problem, you need to evaluate the derivative of the function at x = 1 using the values provided in the table for f(x), g(x), f'(x), and g'(x). This step is crucial for obtaining the final numerical result.
Recommended video:
Function Composition
Function composition involves combining two functions to form a new function, such as f(x) / (g(x) + 1). Understanding how to manipulate and differentiate composed functions is key to solving this problem, as it requires applying the quotient rule to a function that includes a sum in the denominator.
Recommended video:
Evaluate Composite Functions - Special Cases
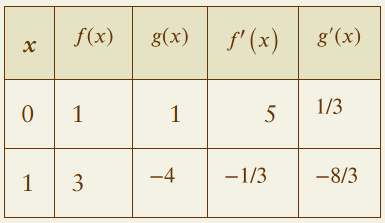
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:

