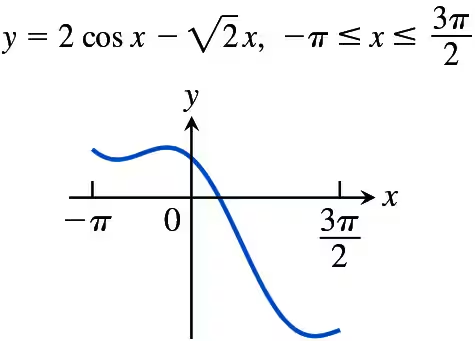
Identify the inflection points and local maxima and minima of the functions graphed in Exercises 1–8. Identify the open intervals on which the functions are differentiable and the graphs are concave up and concave down.
2. y=x^4/4-2x^2+4
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:


 6:02m
6:02mMaster The Second Derivative Test: Finding Local Extrema with a bite sized video explanation from Patrick
Start learning