In Exercises 47 and 48, find an equation for


(a) the tangent line to the curve at P

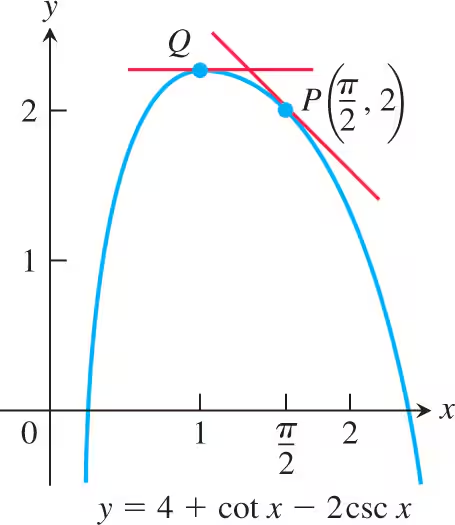
A weight is attached to a spring and reaches its equilibrium position (x = 0). It is then set in motion resulting in a displacement of x = 10 cos t, where x is measured in centimeters and t is measured in seconds. See the accompanying figure.

b. Find the spring’s velocity when t = 0, t = π/3, and t = 3π/4.

Assume that a particle’s position on the x-axis is given by

x = 3 cos t + 4 sin t,

where x is measured in feet and t is measured in seconds.

b. Find the particle’s velocity when t = 0, t = π/2, and t = π.

Tangent Lines

In Exercises 35–38, graph the curves over the given intervals, together with their tangent lines at the given values of x. Label each curve and tangent line with its equation.

y = sin x, −3π/2 ≤ x ≤ 2π

x = −π, 0, 3π/2

Find all points on the curve y = tan x, −π/2 < x < π/2, where the tangent line is parallel to the line y = 2x. Sketch the curve and tangent lines together, labeling each with its equation.

In Exercises 47 and 48, find an equation for

(b) the horizontal tangent line to the curve at Q.

" style="" width="200">

Theory and Examples

The equations in Exercises 49 and 50 give the position s = f(t) of a body moving on a coordinate line (s in meters, t in seconds). Find the body’s velocity, speed, acceleration, and jerk at time t = π/4 sec.

s = 2 − 2 sin t

Is there a value of b that will make

g(x) = { x + b, x < 0

cos x, x ≥ 0

continuous at x = 0? Differentiable at x = 0? Give reasons for your answers.

Find the derivative of the function.

$h\left(t\right)=\sin \left(t\right)\cos \left(t\right)$