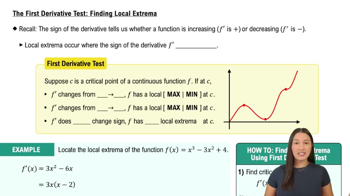
First Derivative Test
a. Locate the critical points of f.
b. Use the First Derivative Test to locate the local maximum and minimum values.
c. Identify the absolute maximum and minimum values of the function on the given interval (when they exist).
f(x) = x² + 3 on [-3,2]