Oblique Asymptotes
Graph the rational functions in Exercises 103–108. Include the graphs and equations of the asymptotes.
y = (x² − 4) / (x − 1)
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: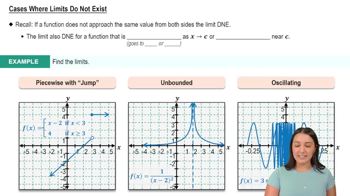
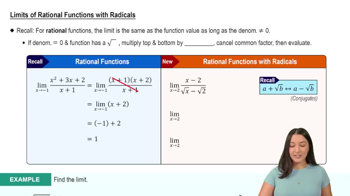


 5:21m
5:21mMaster Finding Limits by Direct Substitution with a bite sized video explanation from Patrick
Start learning