Table of contents

0. Functions7h 52m
1. Limits and Continuity2h 2m
2. Intro to Derivatives1h 33m
3. Techniques of Differentiation3h 18m
4. Applications of Derivatives2h 38m
5. Graphical Applications of Derivatives6h 2m
6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
7. Antiderivatives & Indefinite Integrals1h 26m
8. Definite Integrals4h 44m
9. Graphical Applications of Integrals2h 27m
- Area Between Curves
  1h 18m
- Introduction to Volume & Disk Method
  1h 8m
10. Physics Applications of Integrals 3h 16m
- Kinematics
  1h 13m
- Work
  2h 3m
11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 34m
12. Techniques of Integration7h 39m
13. Intro to Differential Equations2h 55m
14. Sequences & Series5h 36m
15. Power Series2h 19m
- Introduction to Power Series
  1h 9m
- Taylor Series & Taylor Polynomials
  1h 10m
16. Parametric Equations & Polar Coordinates7h 58m

5. Graphical Applications of Derivatives

Finding Global Extrema

Calculus

5. Graphical Applications of Derivatives

Finding Global Extrema

Previous problemNext problem

2:19 minutes

Problem 4.1.5

Textbook Question

Finding Extrema from Graphs

In Exercises 1–6, determine from the graph whether the function has any absolute extreme values on [a, b]. Then explain how your answer is consistent with Theorem 1.

Verified step by step guidance

Examine the graph of the function y = g(x) over the interval [a, b]. Identify any points where the function reaches a maximum or minimum value within this interval.

Notice that the function is continuous on the interval [a, b] except at point c, where there is a discontinuity. The function is not defined at c, as indicated by the open circle.

Identify the endpoints of the interval, a and b, and evaluate the function at these points. These values are potential candidates for absolute extrema.

Look for any local extrema within the interval [a, b] by observing the behavior of the graph. A local maximum or minimum could occur at a point where the graph changes direction.

Apply Theorem 1, which states that if a function is continuous on a closed interval [a, b], it must have an absolute maximum and minimum on that interval. Since the function is not continuous at c, consider only the endpoints and any local extrema that are defined within the interval.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above

Video duration:

Play a video:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Absolute Extrema

Absolute extrema refer to the highest or lowest points on a function within a given interval. An absolute maximum is the highest point, while an absolute minimum is the lowest. These points are crucial in understanding the overall behavior of a function on a specified interval, such as [a, b].

Closed Interval

A closed interval [a, b] includes all the points between a and b, as well as the endpoints themselves. This is important when determining extrema because the function must be evaluated at the endpoints to ensure all possible extreme values are considered, especially if the function is continuous.

Theorem 1 (Extreme Value Theorem)

The Extreme Value Theorem states that if a function is continuous on a closed interval [a, b], it must have both a maximum and minimum value on that interval. This theorem is essential for identifying extrema, as it guarantees their existence under the right conditions, guiding the analysis of the graph.

Watch next

Master Critical Points with a bite sized video explanation from Patrick

Start learning

Related Videos

Related Practice

Textbook Question

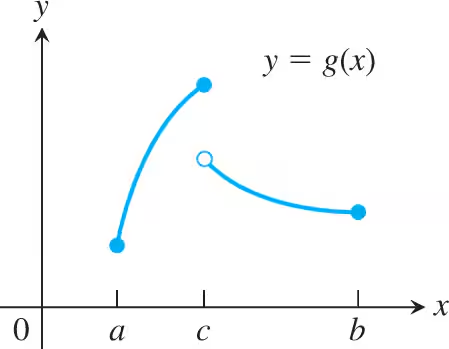
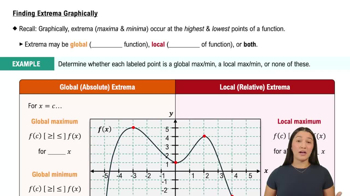
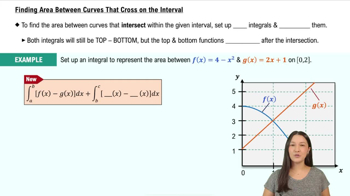
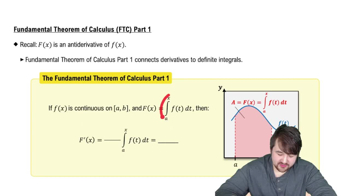
Absolute Extrema on Finite Closed Intervals

In Exercises 21–36, find the absolute maximum and minimum values of each function on the given interval. Then graph the function. Identify the points on the graph where the absolute extrema occur, and include their coordinates.

f(x) = (2/3)x − 5, −2 ≤ x ≤ 3

Textbook Question

Absolute Extrema on Finite Closed Intervals

h(x) = ³√x, −1 ≤ x ≤ 8

Textbook Question

Absolute Extrema on Finite Closed Intervals

g(x) = √(4 − x²), −2 ≤ x ≤ 1

Textbook Question

Absolute Extrema on Finite Closed Intervals

f(t) = 2 − |t|, −1 ≤ t ≤ 3

Textbook Question

Finding Extrema from Graphs

In Exercises 7–10, find the absolute extreme values and where they occur.

Textbook Question

Finding Extrema from Graphs

In Exercises 7–10, find the absolute extreme values and where they occur.

Textbook Question

Finding Extrema from Graphs

In Exercises 15–20, sketch the graph of each function and determine whether the function has any absolute extreme values on its domain. Explain how your answer is consistent with Theorem 1.

f(x) = |x|, −1 < x < 2

Textbook Question

Finding Extrema from Graphs

In Exercises 15–20, sketch the graph of each function and determine whether the function has any absolute extreme values on its domain. Explain how your answer is consistent with Theorem 1.

g(x) = {−x, 0 ≤ x < 1

x − 1, 1 ≤ x ≤ 2

Show more practices

Download the Mobile app

Privacy

Do not sell my personal information

Accessibility

Patent notice

Sitemap

Finding Extrema from GraphsIn Exercises 1–6, determine from the graph whether the function has any absolute extreme values on [a, b]. Then explain how your answer is consistent with Theorem 1.

Key Concepts

Absolute Extrema

Closed Interval

Theorem 1 (Extreme Value Theorem)

Watch next

Finding Extrema from Graphs

In Exercises 1–6, determine from the graph whether the function has any absolute extreme values on [a, b]. Then explain how your answer is consistent with Theorem 1.