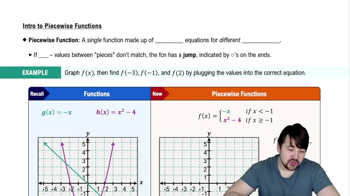
Area functions Let A(x) be the area of the region bounded by the t -axis and the graph of y=ƒ(t) from t=0 to t=x. Consider the following functions and graphs.
a. Find A(2) .
ƒ(t) = {-2t+8 if t ≤ 3 ; 2 if t >3 <IMAGE>
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: