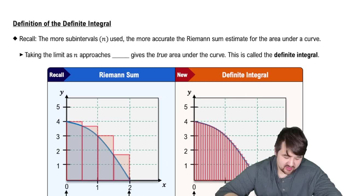
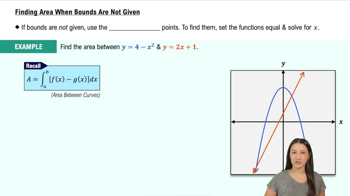
Differentiability and Continuity on an Interval
Each figure in Exercises 45–50 shows the graph of a function over a closed interval D. At what domain points does the function appear to be
c. neither continuous nor differentiable?
Give reasons for your answers.