Absolute maxima and minima Determine the location and value of the absolute extreme values of ƒ on the given interval, if they exist.
ƒ(x) = 2x³ - 15x² + 24x on [0,5]
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: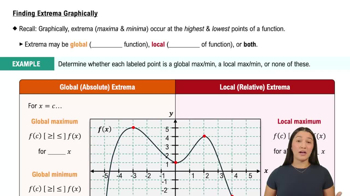



 5:58m
5:58mMaster Finding Extrema Graphically with a bite sized video explanation from Patrick
Start learning