Textbook Question
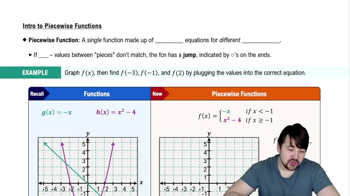
Which of the following functions are continuous for all values in their domain? Justify your answers.
d. p(t)=number of points scored by a basketball player after t minutes of a basketball game
1. Limits and Continuity
Continuity
1:20 minutesProblem 2.6.10
Textbook Question
Evaluate f(3) if lim x→3^− f(x)=5,lim x→3^+ f(x)=6, and f is right-continuous at x=3.
Verified step by step guidance1
Understand the concept of right-continuity: A function f is right-continuous at a point x=a if \( \lim_{x \to a^+} f(x) = f(a) \).
Identify the given information: \( \lim_{x \to 3^-} f(x) = 5 \), \( \lim_{x \to 3^+} f(x) = 6 \), and f is right-continuous at \( x=3 \).
Apply the definition of right-continuity at \( x=3 \): Since f is right-continuous at \( x=3 \), we have \( f(3) = \lim_{x \to 3^+} f(x) \).
Substitute the known limit from the right: \( f(3) = 6 \).
Conclude that the value of \( f(3) \) is determined by the right-hand limit, which is 6.
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Limits
Limits describe the behavior of a function as the input approaches a certain value. In this case, we have left-hand and right-hand limits as x approaches 3, which are 5 and 6, respectively. Understanding limits is crucial for analyzing the continuity and behavior of functions at specific points.
Recommended video:
05:50
One-Sided Limits
Right-Continuity
A function is right-continuous at a point if the limit of the function as it approaches that point from the right equals the function's value at that point. In this scenario, since f is right-continuous at x=3, it implies that f(3) must equal the right-hand limit, which is 6.
Recommended video:
05:34Intro to Continuity
Piecewise Functions
Piecewise functions are defined by different expressions based on the input value. In this question, the function f has different behaviors approaching from the left and right of x=3, which is a common scenario in piecewise definitions. Understanding how to evaluate such functions is essential for determining their values at specific points.
Recommended video:
05:36Piecewise Functions
Related Videos
Related Practice