Inverse of composite functions
a. Let g(x) = 2x + 3 and h(x) = x³. Consider the composite function ƒ(x) = g(h(x)). Find ƒ⁻¹ directly and then express it in terms of g⁻¹ and h⁻¹
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:

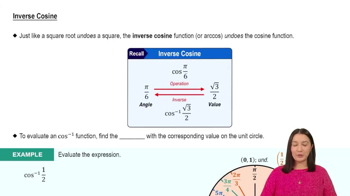

 5:57m
5:57mMaster Graphs of Common Functions with a bite sized video explanation from Patrick
Start learning