A bug is moving along the right side of the parabola y=x² at a rate such that its distance from the origin is increasing at 1 cm/min.
b. Use the equation y=x² to find an equation relating dy/dt to dx/dt.
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: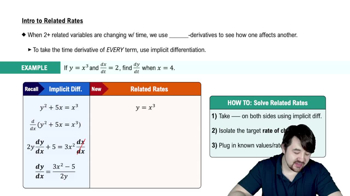


 4:16m
4:16mMaster Intro To Related Rates with a bite sized video explanation from Patrick
Start learning