Find the limit using the graph of shown.
Table of contents
- 0. Functions7h 55m
- Introduction to Functions18m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 31m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
1. Limits and Continuity
Introduction to Limits
Struggling with Calculus?
Join thousands of students who trust us to help them ace their exams!Watch the first videoMultiple Choice
Using the graph, find the specified limit or state that the limit does not exist.
limx→4−f(x), limx→4+f(x), limx→4f(x)
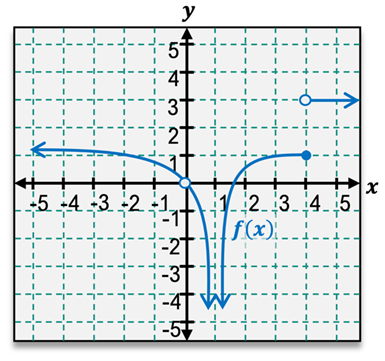
A
limx→4−f(x)=1, limx→4+f(x)=1, limx→4f(x)=1
B
limx→4−f(x)=3, limx→4+f(x)=3, limx→4f(x)=3
C
limx→4−f(x)=3, limx→4+f(x)=1, limx→4f(x)=DNE
D
limx→4−f(x)=1, limx→4+f(x)=3, limx→4f(x)=DNE
0 Comments
 Verified step by step guidance
Verified step by step guidance1
Examine the graph of the function f(x) as x approaches 4 from the left (x → 4⁻). Notice that the graph approaches the y-value of 1 as x gets closer to 4 from the left side.
Now, examine the graph as x approaches 4 from the right (x → 4⁺). Observe that the graph approaches the y-value of 3 as x gets closer to 4 from the right side.
Since the left-hand limit (x → 4⁻) is 1 and the right-hand limit (x → 4⁺) is 3, the two one-sided limits are not equal.
For the limit as x approaches 4 (x → 4) to exist, the left-hand limit and the right-hand limit must be equal. Since they are not equal, the limit as x approaches 4 does not exist.
Therefore, the correct interpretation of the graph is: lim(x→4⁻)f(x) = 1, lim(x→4⁺)f(x) = 3, and lim(x→4)f(x) = DNE (does not exist).

 6:47m
6:47mWatch next
Master Finding Limits Numerically and Graphically with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Multiple Choice
Introduction to Limits practice set


