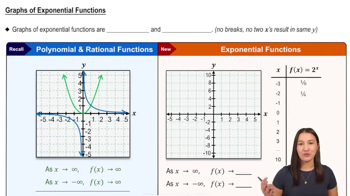
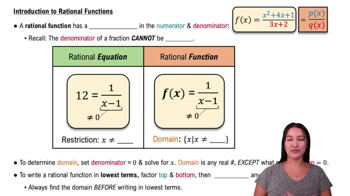
Limits and Infinity
Find the limits in Exercises 37–46.
x⁴ + x³
lim -----------------
x→∞ 12x³ + 128
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:

 5:21m
5:21mMaster Finding Limits by Direct Substitution with a bite sized video explanation from Patrick
Start learning