The intensity of illumination at any point from a light source is proportional to the square of the reciprocal of the distance between the point and the light source. Two lights, one having an intensity eight times that of the other, are 6 m apart. How far from the stronger light is the total illumination least?
Table of contents
- 0. Functions7h 54m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 31m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
5. Graphical Applications of Derivatives
Applied Optimization
Problem 4.5.52a
Textbook Question
52. Two masses hanging side by side from springs have positions s_1 = 2 sin t and s_2 = sin 2t,
respectively.
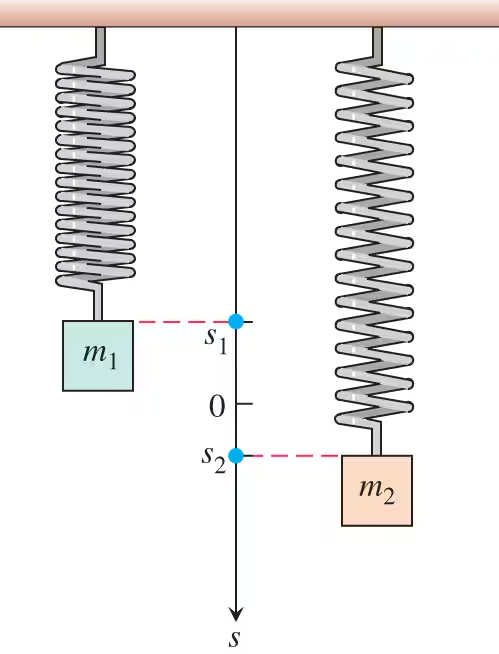
a. At what times in the interval 0 < t do the masses pass each other? (Hint: sin 2t = 2 sint cost.)
 Verified step by step guidance
Verified step by step guidance1
To find the times when the masses pass each other, we need to set their positions equal: s_1 = s_2. Given s_1 = 2 sin t and s_2 = sin 2t, we equate them: 2 sin t = sin 2t.
Use the hint provided: sin 2t = 2 sin t cos t. Substitute this into the equation: 2 sin t = 2 sin t cos t.
Simplify the equation by dividing both sides by 2 sin t, assuming sin t is not zero: 1 = cos t.
Solve the equation 1 = cos t for t in the interval 0 < t. The cosine function equals 1 at t = 0, but we need to find other solutions within the interval.
Since cos t = 1 at t = 0 and t = 2π, within the interval 0 < t, the solution is t = 2π. However, check for other possible solutions within the given interval.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
11mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Trigonometric Functions
Trigonometric functions, such as sine and cosine, are fundamental in calculus and physics, representing periodic phenomena. In this problem, the positions of the masses are given by sine functions, which oscillate between -1 and 1. Understanding how these functions behave over time is crucial for determining when the two masses pass each other.
Recommended video:

Introduction to Trigonometric Functions
Equating Positions
To find when the two masses pass each other, we need to set their position equations equal to each other: s_1 = s_2. This involves solving the equation 2 sin(t) = sin(2t). This step is essential as it translates the physical scenario into a mathematical problem that can be solved using algebraic techniques.
Recommended video:
Solving Logarithmic Equations
Double Angle Identity
The double angle identity for sine states that sin(2t) = 2 sin(t) cos(t). This identity simplifies the equation we need to solve, allowing us to express sin(2t) in terms of sin(t) and cos(t). Utilizing this identity is a key step in solving the problem, as it helps to reduce the complexity of the equation.
Recommended video:
Solve Trig Equations Using Identity Substitutions

 1:13m
1:13mWatch next
Master Intro to Applied Optimization: Maximizing Area with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
