What are the three Pythagorean identities for the trigonometric functions?
Table of contents
- 0. Functions7h 54m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 31m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
0. Functions
Trigonometric Identities
Problem 63
Textbook Question
A triangle has side c = 2 and angles A = π/4 and B = π/3. Find the length a of the side opposite A.
 Verified step by step guidance
Verified step by step guidance1
First, recognize that you are dealing with a triangle where you know two angles and one side. This is a case for the Law of Sines, which relates the sides of a triangle to the sines of its angles.
The Law of Sines states: \( \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} \). In this problem, you need to find side 'a', and you know side 'c' and angles A and B.
Calculate the third angle C using the fact that the sum of angles in a triangle is \( \pi \) radians. So, \( C = \pi - A - B \). Substitute \( A = \frac{\pi}{4} \) and \( B = \frac{\pi}{3} \) to find \( C \).
Now, apply the Law of Sines: \( \frac{a}{\sin A} = \frac{c}{\sin C} \). Substitute the known values: \( c = 2 \), \( A = \frac{\pi}{4} \), and the calculated \( C \).
Solve for 'a' by rearranging the equation: \( a = c \cdot \frac{\sin A}{\sin C} \). Substitute the values and calculate the sine of the angles to find the length of side 'a'.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Law of Sines
The Law of Sines states that the ratio of the length of a side of a triangle to the sine of its opposite angle is constant for all three sides and angles. This relationship can be expressed as a/sin(A) = b/sin(B) = c/sin(C). In this problem, it allows us to find the unknown side 'a' by relating it to the known side 'c' and the angles A and B.
Recommended video:
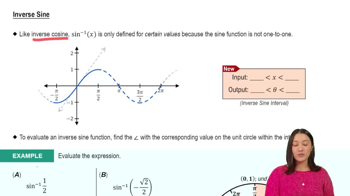
Inverse Sine
Angle Measures in Radians
In calculus and trigonometry, angles can be measured in degrees or radians. Radians are a more natural unit for mathematical analysis, where π radians equals 180 degrees. Understanding how to convert between these two systems is crucial, especially since the angles given in the problem are in radians, which will be used in the sine function calculations.
Recommended video:
Guided course
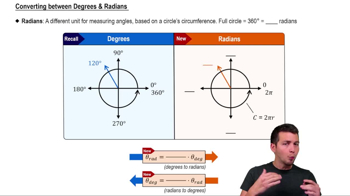
Converting between Degrees & Radians
Trigonometric Functions
Trigonometric functions, such as sine, cosine, and tangent, relate the angles of a triangle to the ratios of its sides. The sine function, in particular, is essential for solving triangles, as it provides a way to calculate unknown side lengths when angles are known. In this problem, we will use the sine of angles A and B to find the length of side 'a' opposite angle A.
Recommended video:

Introduction to Trigonometric Functions

 6:36m
6:36mWatch next
Master Simplifying Trig Expressions with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
