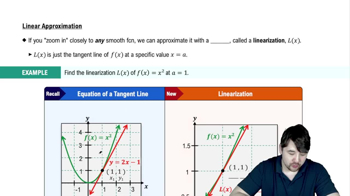
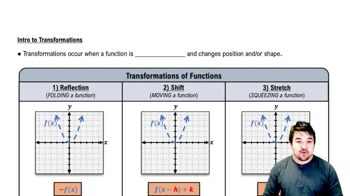
Graph ƒ₁ and ƒ₂ together. Then describe how applying the absolute value function in ƒ₂ affects the graph of ƒ₁.
ƒ₁(x) ƒ₂(x)
__ ___
√ x √ |x|
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:

 5:56m
5:56mMaster Adding & Subtracting Functions with a bite sized video explanation from Patrick
Start learning