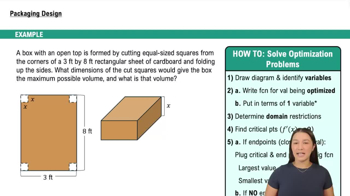
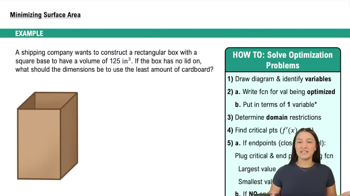
Travel costs A simple model for travel costs involves the cost of gasoline and the cost of a driver. Specifically, assume gasoline costs \(p/gallon and the vehicle gets g miles per gallon. Also assume the driver earns \)w/hour.
b. At what speed does the gas mileage function have its maximum?