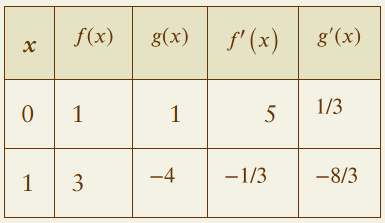Suppose that functions f and g and their derivatives with respect to x have the following values at x = 2 and x = 3.
" style="" width="250">
Find the derivatives with respect to x of the following combinations at the given value of x.
f. √f(x), x = 2