Using the piecewise function below, evaluate
Table of contents
- 0. Functions7h 54m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 31m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
0. Functions
Piecewise Functions
Problem 1.1.29b
Textbook Question
Piecewise-Defined Functions
Find a formula for each function graphed in Exercises 29–32.
b. <IMAGE>
 Verified step by step guidance
Verified step by step guidance1
Identify the different segments of the piecewise function from the graph. Look for changes in the slope or direction of the graph, as well as any discontinuities or breaks.
For each segment, determine the type of function it represents (e.g., linear, quadratic, constant). This can often be done by observing the shape of the graph.
Write the equation for each segment. For a linear segment, use the slope-intercept form \( y = mx + b \), where \( m \) is the slope and \( b \) is the y-intercept. For other types of functions, use the appropriate form.
Determine the domain for each segment. This involves identifying the x-values over which each segment is defined. Pay attention to open and closed intervals, which are indicated by open or closed circles on the graph.
Combine the equations and their respective domains into a piecewise function. Use the format: \( f(x) = \begin{cases} \text{equation 1,} & \text{if } \text{domain 1} \\ \text{equation 2,} & \text{if } \text{domain 2} \\ \end{cases} \).
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Piecewise-Defined Functions
A piecewise-defined function is a function composed of multiple sub-functions, each of which applies to a specific interval of the domain. These functions are defined by different expressions based on the input value. Understanding how to interpret and construct these functions is crucial for analyzing graphs that change behavior at certain points.
Recommended video:
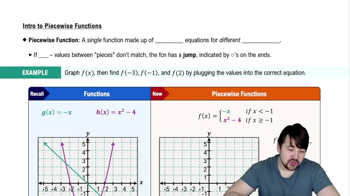
Piecewise Functions
Graph Interpretation
Interpreting a graph involves understanding the visual representation of a function, including identifying key features such as intercepts, slopes, and discontinuities. For piecewise functions, it's essential to recognize where the function changes its rule and how each segment corresponds to a different part of the function's definition.
Recommended video:
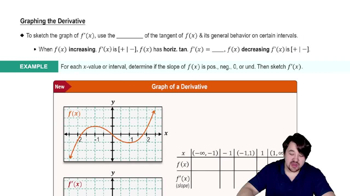
Graphing The Derivative
Function Formulation
Formulating a function from a graph requires translating visual information into mathematical expressions. This involves determining the equations for each segment of the graph, considering the slope and y-intercept for linear parts, and ensuring continuity or identifying points of discontinuity where applicable.
Recommended video:

Properties of Functions
Related Videos
Related Practice
Multiple Choice


