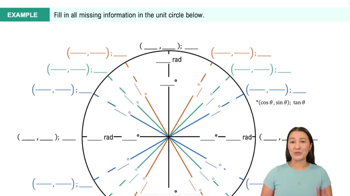
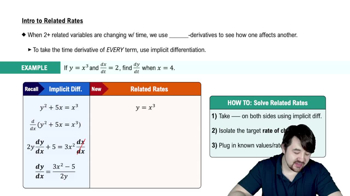
Tracking a dive A biologist standing at the bottom of an 80-foot vertical cliff watches a peregrine falcon dive from the top of the cliff at a 45° angle from the horizontal (see figure). <IMAGE>
b. What is the rate of change of θ with respect to the bird’s height when it is 60 ft above the ground?