Suppose the objective function P= xy is subject to the constraint 10x + y = 100, where x and y are real numbers.
a. Eliminate the variable y from the objective function so that P is expressed as a function of one variable x.
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: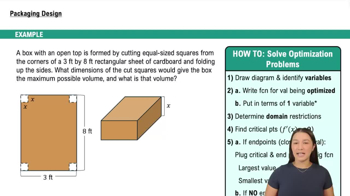


 1:13m
1:13mMaster Intro to Applied Optimization: Maximizing Area with a bite sized video explanation from Patrick
Start learning