The position (in meters) of a marble, given an initial velocity and rolling up a long incline, is given by s = 100t / t+1, where t is measured in seconds and s=0 is the starting point.
b. Find the velocity function for the marble.
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: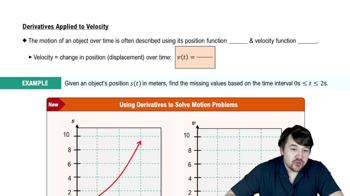


 6:29m
6:29mMaster Derivatives Applied To Velocity with a bite sized video explanation from Patrick
Start learning