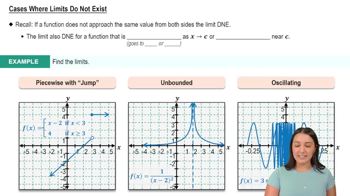
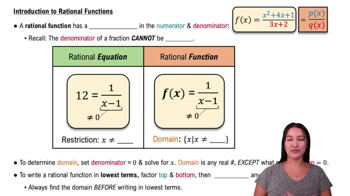
Limits as x → ∞ or x → −∞
The process by which we determine limits of rational functions applies equally well to ratios containing noninteger or negative powers of x. Divide numerator and denominator by the highest power of x in the denominator and proceed from there. Find the limits in Exercises 23–36. Write ∞ or −∞ where appropriate.
lim x→∞ (2√x + x⁻¹) / (3x − 7)