Water flows into a conical tank at a rate of 2 ft³/min. If the radius of the top of the tank is 4 ft and the height is 6 ft, determine how quickly the water level is rising when the water is 2 ft deep in the tank.

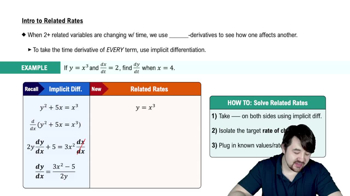
An angler hooks a trout and begins turning her circular reel at 1.5 rev/s. Assume the radius of the reel (and the fishing line on it) is 2 inches.

a. Let R equal the number of revolutions the angler has turned her reel and suppose L is the amount of line that she has reeled in. Find an equation for L as a function of R.

Robert Boyle (1627–1691) found that for a given quantity of gas at a constant temperature, the pressure P (in kPa) and volume V of the gas (in m³) are accurately approximated by the equation V=k/P, where k>0 is constant. Suppose the volume of an expanding gas is increasing at a rate of 0.15 m³/min when the volume V=0.5 m³ and the pressure is P=50 kPa. At what rate is pressure changing at this moment?

Two boats leave a port at the same time, one traveling west at 20 mi/hr and the other traveling southwest ( 45° south of west) at 15 mi/hr. After 30 minutes, how far apart are the boats and at what rate is the distance between them changing? (Hint: Use the Law of Cosines.)

A spherical balloon is inflated at a rate of 10 cm³/min. At what rate is the diameter of the balloon increasing when the balloon has a diameter of 5 cm?

A jet flying at 450 mi/hr and traveling in a straight line at a constant elevation of 500 ft passes directly over a spectator at an air show. How quickly is the angle of elevation (between the ground and the line from the spectator to the jet) changing 2 seconds later? 

Watching an elevator An observer is 20 m above the ground floor of a large hotel atrium looking at a glass-enclosed elevator shaft that is 20 m horizontally from the observer (see figure). The angle of elevation of the elevator is the angle that the observer’s line of sight makes with the horizontal (it may be positive or negative). Assuming the elevator rises at a rate of 5 m/s, what is the rate of change of the angle of elevation when the elevator is 10 m above the ground? When the elevator is 40 m above the ground? <IMAGE>

The bottom of a large theater screen is 3 ft above your eye level and the top of the screen is 10 ft above your eye level. Assume you walk away from the screen (perpendicular to the screen) at a rate of 3 ft/s while looking at the screen. What is the rate of change of the viewing angle θ when you are 30 ft from the wall on which the screen hangs, assuming the floor is horizontal (see figure)? <IMAGE>

A ship leaves port traveling southwest at a rate of 12 mi/hr. At noon, the ship reaches its closest approach to a radar station, which is on the shore 1.5 mi from the port. If the ship maintains its speed and course, what is the rate of change of the tracking angle θ between the radar station and the ship at 1:30 P.M. (see figure)? (Hint: Use the Law of Sines.) <IMAGE>