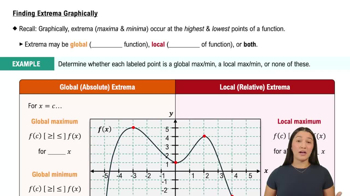
Identifying Extrema
In Exercises 63 and 64, the graph of f' is given. Assume that f has domain (-2, 2).
" style="" width="220">
a. Either use the graph to determine which intervals f is increasing on and which intervals f is decreasing on, or explain why this information cannot be determined from the graph.