Show that the linearization of f(x) = (1 + x)ᵏ at x = 0 is L(x) = 1 + kx.

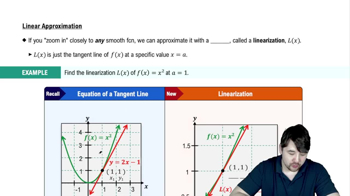
Linearization for Approximation

In Exercises 7–12, find a linearization at a suitably chosen integer near a at which the given function and its derivative are easy to evaluate.

f(x) = ∛x, a = 8.5

Use the linear approximation (1 + x)ᵏ ≈ 1 + kx to find an approximation for the function f(x) for values of x near zero.

a. f(x) = (1 − x)⁶

Use the linear approximation (1 + x)ᵏ ≈ 1 + kx to find an approximation for the function f(x) for values of x near zero.

c. f(x) = 1/√(1 + x)

Faster than a calculator Use the approximation (1 + x)ᵏ ≈ 1 + kx to estimate the following.

a. (1.0002)⁵⁰

If $f\left(x\right)=x^3+1$, use the linearization $L\left(x\right)$ at $a=5$ to approximate $f\left(5.1\right)$.

If $f\left(x\right)=\sqrt{x}+12$, use the linearization $L\left(x\right)$ at $a=16$ to approximate $f\left(16.01\right)$.

21–32. Mean Value Theorem Consider the following functions on the given interval [a, b].

a. Determine whether the Mean Value Theorem applies to the following functions on the given interval [a, b].

b. If so, find the point(s) that are guaranteed to exist by the Mean Value Theorem.

ƒ(x) = { - 2x if x < 0 ; x if x ≥ 0 ; [-1, 1]

21–32. Mean Value Theorem Consider the following functions on the given interval [a, b].

a. Determine whether the Mean Value Theorem applies to the following functions on the given interval [a, b].

b. If so, find the point(s) that are guaranteed to exist by the Mean Value Theorem.

ƒ(x) = 7 -x² ; [-1; 2]