Theory and Examples
Cubic functions Consider the cubic function f(x) = ax³ + bx² + cx + d.
b. How many local extreme values can f have?
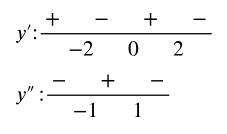
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:



 7:32m
7:32mMaster Determining Where a Function is Increasing & Decreasing with a bite sized video explanation from Patrick
Start learning