Table of contents

0. Functions7h 52m
1. Limits and Continuity2h 2m
2. Intro to Derivatives1h 33m
3. Techniques of Differentiation3h 18m
4. Applications of Derivatives2h 38m
5. Graphical Applications of Derivatives6h 2m
6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
7. Antiderivatives & Indefinite Integrals1h 26m
8. Definite Integrals4h 44m
9. Graphical Applications of Integrals2h 27m
- Area Between Curves
  1h 18m
- Introduction to Volume & Disk Method
  1h 8m
10. Physics Applications of Integrals 3h 16m
- Kinematics
  1h 13m
- Work
  2h 3m
11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 34m
12. Techniques of Integration7h 39m
13. Intro to Differential Equations2h 55m
14. Sequences & Series5h 36m
15. Power Series2h 19m
- Introduction to Power Series
  1h 9m
- Taylor Series & Taylor Polynomials
  1h 10m
16. Parametric Equations & Polar Coordinates7h 58m

1. Limits and Continuity

Introduction to Limits

Calculus

1. Limits and Continuity

Introduction to Limits

Previous problemNext problem

2:50 minutes

Problem 2.4.53b

Textbook Question

Determine whether the following statements are true and give an explanation or counterexample.
The line x=−1 is a vertical asymptote of the function f(x) =x^2 − 7x + 6 / x^2 − 1.

Verified step by step guidance

Step 1: Identify the function f(x) = \frac{x^2 - 7x + 6}{x^2 - 1}. This is a rational function, which means it is a fraction where both the numerator and the denominator are polynomials.

Step 2: Determine the points where the denominator is zero, as these are potential vertical asymptotes. Set the denominator equal to zero: x^2 - 1 = 0.

Step 3: Solve the equation x^2 - 1 = 0. This can be factored as (x - 1)(x + 1) = 0, giving the solutions x = 1 and x = -1.

Step 4: Check if x = -1 is a vertical asymptote by ensuring it is not a removable discontinuity. Factor the numerator: x^2 - 7x + 6 = (x - 1)(x - 6).

Step 5: Since x = -1 does not cancel out with any factor in the numerator, it is indeed a vertical asymptote. Therefore, the statement is true.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above

Video duration:

Play a video:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Vertical Asymptotes

A vertical asymptote occurs in a function when the function approaches infinity or negative infinity as the input approaches a certain value. This typically happens at values of x that make the denominator of a rational function equal to zero, provided that the numerator does not also equal zero at that point.

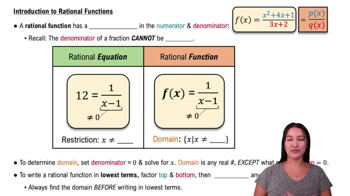
Rational Functions

A rational function is a function that can be expressed as the ratio of two polynomials. The general form is f(x) = P(x)/Q(x), where P and Q are polynomials. Understanding the behavior of rational functions, especially their asymptotic behavior, is crucial for analyzing their graphs and determining points of discontinuity.

Factoring Polynomials

Factoring polynomials involves rewriting a polynomial as a product of its factors, which can simplify the analysis of functions. For example, the function f(x) = (x^2 - 7x + 6)/(x^2 - 1) can be factored to identify points where the function is undefined, helping to determine the presence of vertical asymptotes.

Watch next

Master Finding Limits Numerically and Graphically with a bite sized video explanation from Patrick

Start learning

Related Videos

Related Practice

Textbook Question

Analyze the following limits. Then sketch a graph of y=tanx with the window [−π,π]×[−10,10]and use your graph to check your work.

lim x→π/2^− tan x

Textbook Question

Analyze the following limits. Then sketch a graph of y=tanx with the window [−π,π]×[−10,10]and use your graph to check your work.

lim x→π/2^+ tan x

Textbook Question

Analyze the following limits. Then sketch a graph of y=tanx with the window [−π,π]×[−10,10]and use your graph to check your work.

lim x→π/2^− tan x

Textbook Question

Find polynomials p and q such that f=p/q is undefined at 1 and 2, but f has a vertical asymptote only at 2. Sketch a graph of your function.

Textbook Question

Use analytical methods and/or a graphing utility to identify the vertical asymptotes (if any) of the following functions.

f(x)=x^2−3x+2 / x^10−x^9

Textbook Question

Use analytical methods and/or a graphing utility to identify the vertical asymptotes (if any) of the following functions.

h(x)=e^x(x+1)^3

Textbook Question

Use analytical methods and/or a graphing utility to identify the vertical asymptotes (if any) of the following functions.

g(θ)=tan πθ/10

Textbook Question

Use analytical methods and/or a graphing utility to identify the vertical asymptotes (if any) of the following functions.

f(x)=1/ √x sec x

Show more practices

Download the Mobile app

Privacy

Do not sell my personal information

Accessibility

Patent notice

Sitemap

Determine whether the following statements are true and give an explanation or counterexample.The line x=−1 is a vertical asymptote of the function f(x) =x^2 − 7x + 6 / x^2 − 1.

Key Concepts

Vertical Asymptotes

Rational Functions

Factoring Polynomials

Watch next

Determine whether the following statements are true and give an explanation or counterexample.
The line x=−1 is a vertical asymptote of the function f(x) =x^2 − 7x + 6 / x^2 − 1.