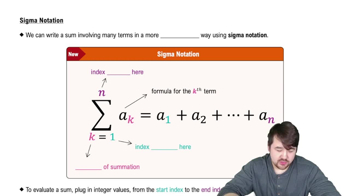
Analyzing slopes Use the points A, B, C, D, and E in the following graphs to answer these questions. <IMAGE>
a. At which points is the slope of the curve negative?
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:


 6:21m
6:21mMaster Properties of Functions with a bite sized video explanation from Patrick
Start learning